Suction pressure is the force per unit area at your pump’s inlet, measured in PSI or bar. Calculate it using this formula: Suction Pressure = Atmospheric Pressure + Static Head Pressure – Friction Losses.

This guide breaks down each calculation step, shows you how seal chamber pressure relates to suction conditions, and provides the practical tools you need to keep your pumps running.

Suction Pressure Basics

Suction pressure determines whether your pump can pull fluid effectively without damaging itself. It’s the total pressure available at the pump inlet when the system is running.

Think of it as the pushing force that helps fluid enter your pump. Too little pressure causes cavitation—vapor bubbles that collapse violently and destroy impellers and seals.

Every pump has a minimum suction pressure requirement called Net Positive Suction Head Required (NPSHr). Your calculated suction pressure must exceed this value, typically by at least 3 feet of head or 10%.

The Core Formula and Components

The complete suction pressure formula accounts for three main forces:

Ps = Pa + Hs - Hf

Where:

• Ps = Suction pressure (absolute)
• Pa = Atmospheric pressure (14.7 PSI at sea level)
• Hs = Static head pressure
• Hf = Friction losses

Static head pressure comes from the liquid height above your pump centerline. Calculate it by multiplying the vertical distance in feet by the fluid’s specific gravity, then by 0.433 to convert to PSI.

Step-by-Step Calculation Process

Step 1

Measure the vertical distance from your liquid surface to the pump centerline. If the tank is above the pump, this creates positive head. If below, it’s negative (suction lift).

Step 2

Convert this height to pressure. For water: Height (ft) × 0.433 = PSI. For other fluids, multiply by their specific gravity first.

Step 3

Calculate friction losses using manufacturer’s charts or this simplified formula:

Hf = (f × L × V²)/(2 × g × D)

Where:

• f is the friction factor
• L is pipe length
• V is velocity
• g is gravity
• D is pipe diameter

Step 4

Add atmospheric pressure (14.7 PSI at sea level, less at higher elevations).

Step 5

Subtract friction losses from your total to get final suction pressure.

Practical Examples

Example 1: Open Tank Above Pump

• Tank level: 20 feet above pump
• Fluid: Water at 70°F
• Pipe: 50 feet of 4-inch diameter
• Flow rate: 500 GPM

Static head: 20 ft × 0.433 = 8.66 PSI

Friction loss (from tables): 1.2 PSI

Atmospheric pressure: 14.7 PSI

Suction pressure = 14.7 + 8.66 – 1.2 = 22.16 PSI absolute

Example 2: Suction Lift Condition

• Source: 15 feet below pump
• Fluid: Water at 180°F
• Vapor pressure: 7.5 PSI

Static head: -15 ft × 0.433 = -6.5 PSI

FAQs

What’s the difference between suction pressure and seal chamber pressure?

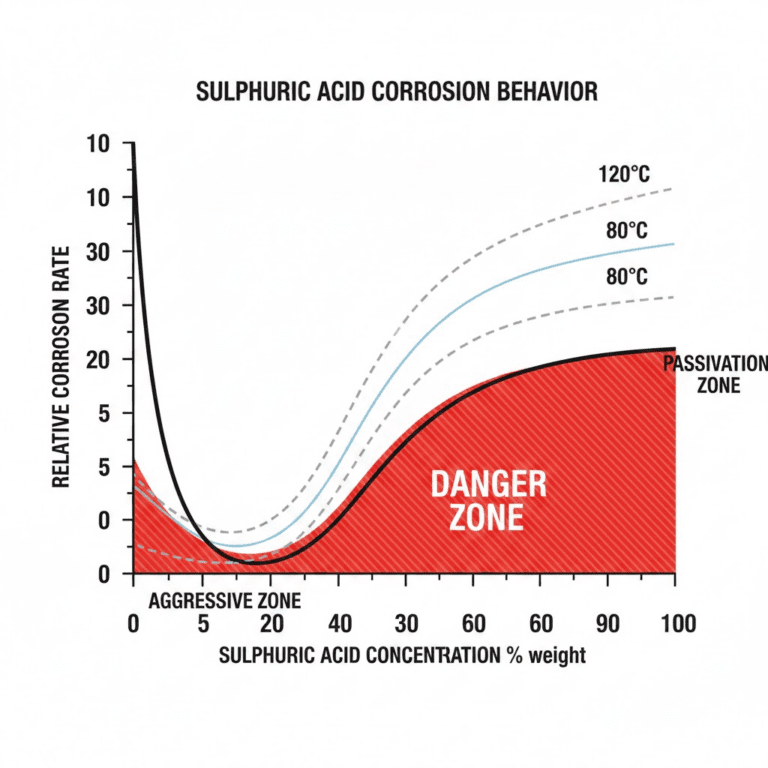
Suction pressure measures force at the pump inlet, while seal chamber pressure is the force inside the seal housing. Seal chamber pressure typically exceeds suction pressure due to impeller action, affecting mechanical seal performance and life.

How do I convert suction pressure to NPSH?

Convert absolute suction pressure to feet of head by dividing PSI by (0.433 × specific gravity). Subtract vapor pressure head and velocity head. This gives you Net Positive Suction Head Available (NPSHA).

Why does my suction pressure calculation differ from gauge readings?

Gauge readings show relative pressure, not absolute. Add atmospheric pressure (14.7 PSI at sea level) to gauge readings. Also check for measurement location errors—gauges too far from the pump show different values.

What suction pressure do mechanical seals need?

Most mechanical seals require positive suction pressure to prevent flashing at seal faces. Minimum seal chamber pressure varies by seal type but typically needs 10-15 PSI above vapor pressure for reliable operation.

How does fluid temperature affect my calculations?

Higher temperatures increase vapor pressure, reducing available NPSH. For every 10°F increase in water temperature above 60°F, subtract approximately 0.5 feet from available suction head to maintain safe margins.